core.base_calculus.Operation Class Reference

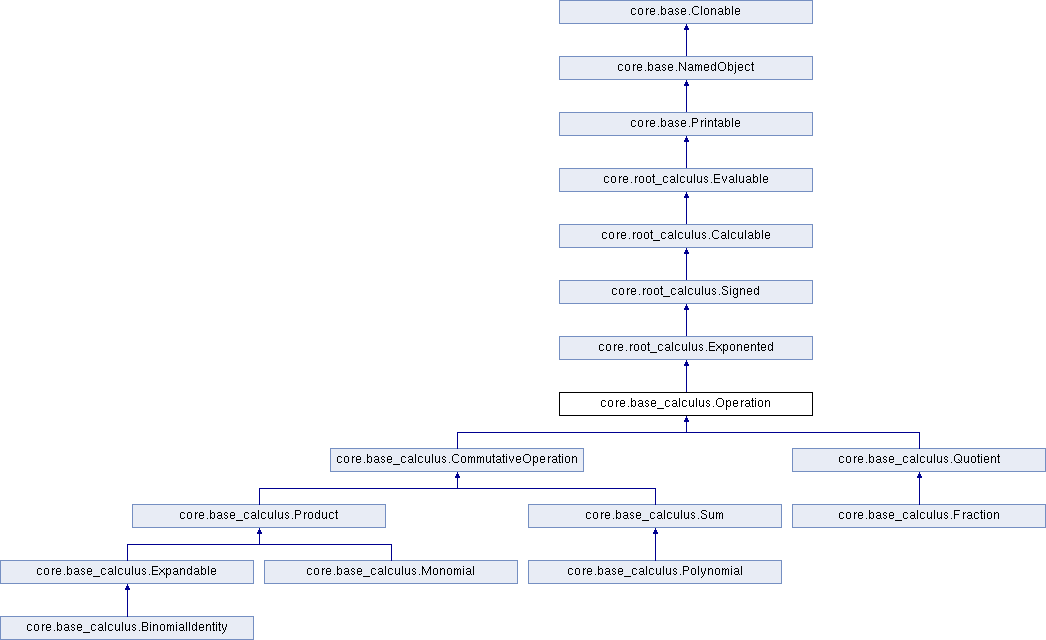
Abstract mother class of Quotient and of CommutativeOperation. More...

Inheritance diagram for core.base_calculus.Operation:

List of all members.

Public Member Functions
def	__init__
	Constructor.
def	get_element
	Returns the list of elements.
def	get_neutral
	Returns the list of elements to iter over.
def	get_symbol
	Returns the symbol field of the Operation.
def	get_iteration_list
	Returns the list of elements to iter over.
def	set_element
def	set_symbol
	Resets the element field.
def	reset_element
	Resets the element field.
def	__hash__
	Makes any Operation hashable (so, usable as dictionnary keys)
def	__getitem__
	It is possible to index an CommutativeOperation.
def	__setitem__
def	operator
	Defines the performed CommutativeOperation.
def	is_expandable
	True if the Operation contains any Expandable.
def	is_numeric
	True if the Operation contains only numeric elements.
def	is_literal
	True if the Operation contains only literal terms.
Properties
	element
	neutral
	symbol

---

Detailed Description

Abstract mother class of Quotient and of CommutativeOperation.

Definition at line 1861 of file base_calculus.py.

---

Constructor & Destructor Documentation

def core.base_calculus.Operation.__init__

(

self

)

Constructor.

Warning:

Operation objects are not really usable

Returns:

An "instance" of Operation

Reimplemented from core.root_calculus.Exponented.

Reimplemented in core.base_calculus.CommutativeOperation.

Definition at line 1872 of file base_calculus.py.

References core.base_calculus.Operation._element, core.base_calculus.Operation._neutral, and core.base_calculus.Operation._symbol.

Referenced by core.calculus.Equation.__init__(), and core.root_calculus.Value.substitute().

---

Member Function Documentation

def core.base_calculus.Operation.__hash__

(

self

)

Makes any Operation hashable (so, usable as dictionnary keys)

Warning:

Seems that subclasses that redefine __eq__() are forgetting __hash__()

Reimplemented in core.base_calculus.Product.

Definition at line 1994 of file base_calculus.py.

References core.base_calculus.Operation.element, core.base_calculus.Item.sign, core.root_calculus.Signed.sign, core.root_calculus.Value.sign, core.base_calculus.SquareRoot.sign, core.base_calculus.Quotient.sign, core.base_calculus.Fraction.sign, core.base_calculus.Monomial.sign, and core.base_calculus.Operation.symbol.

def core.base_calculus.Operation.is_expandable

(

self

)

True if the Operation contains any Expandable.

Returns:

True|False

Reimplemented in core.base_calculus.Expandable.

Definition at line 2032 of file base_calculus.py.

def core.base_calculus.Operation.set_element	(		self,
			n,
			arg
	)

Parameters:

n	: number of the element to set
arg	: the object to put as n-th element

Definition at line 1955 of file base_calculus.py.

References core.base_calculus.Operation._element.

Referenced by core.base_calculus.Product.set_factor(), and core.base_calculus.Sum.set_term().

---

Property Documentation

core::base_calculus.Operation::element [static]

Initial value:

property(get_element,
                       doc = "element field of Operation")

Definition at line 1937 of file base_calculus.py.

Referenced by core.base_calculus.Operation.__hash__(), core.base_calculus.Product.__hash__(), core.base_calculus.Monomial.__init__(), core.base_calculus.CommutativeOperation.__len__(), core.base_calculus.CommutativeOperation.contains_exactly(), core.base_calculus.CommutativeOperation.dbg_str(), core.base_calculus.CommutativeOperation.evaluate(), core.base_calculus.Product.get_factors_list(), core.base_calculus.CommutativeOperation.get_first_letter(), core.base_calculus.Operation.get_iteration_list(), core.base_calculus.Sum.get_literal_terms(), core.base_calculus.Product.get_minus_signs_nb(), core.base_calculus.Sum.get_numeric_terms(), core.base_calculus.CommutativeOperation.get_sign(), core.base_calculus.Sum.get_terms_lexicon(), core.base_calculus.Product.into_str(), core.base_calculus.Product.is_displ_as_a_single_0(), core.base_calculus.Sum.is_displ_as_a_single_1(), core.base_calculus.Product.is_displ_as_a_single_minus_1(), core.base_calculus.Sum.is_displ_as_a_single_minus_1(), core.base_calculus.CommutativeOperation.is_displ_as_a_single_neutral(), core.base_calculus.CommutativeOperation.is_displ_as_a_single_numeric_Item(), core.base_calculus.Monomial.is_negative(), core.base_calculus.Product.is_null(), core.base_calculus.Monomial.is_positive(), core.base_calculus.CommutativeOperation.remove(), core.base_calculus.Monomial.set_letter(), and core.base_calculus.CommutativeOperation.throw_away_the_neutrals().

core::base_calculus.Operation::neutral [static]

Initial value:

property(get_neutral,
                       doc = "neutral field of Operation")

Definition at line 1940 of file base_calculus.py.

Referenced by core.base_calculus.CommutativeOperation.evaluate(), core.base_calculus.Product.into_str(), and core.base_calculus.CommutativeOperation.throw_away_the_neutrals().

core::base_calculus.Operation::symbol [static]

Initial value:

property(get_symbol,
                      doc = "symbol field of Operation")

Definition at line 1943 of file base_calculus.py.

Referenced by core.base_calculus.Operation.__hash__(), core.base_calculus.Product.__hash__(), core.base_calculus.Quotient.calculate_next_step(), core.base_calculus.CommutativeOperation.dbg_str(), and core.base_calculus.Quotient.into_str().

---

The documentation for this class was generated from the following file:

• mamk_misc/doc/mathmaker4doxygen/core/base_calculus.py