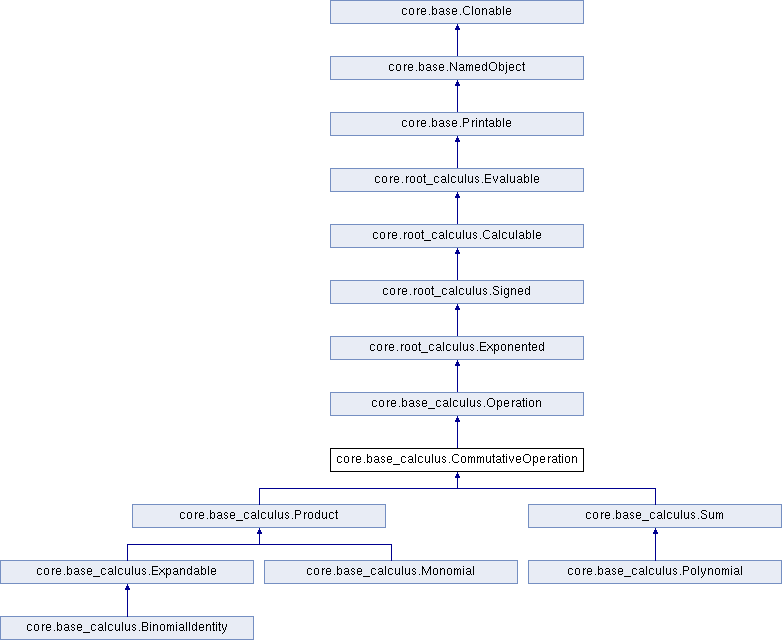
Abstract mother class of Product and Sum. More...

Inheritance diagram for core.base_calculus.CommutativeOperation:

Public Member Functions
def	__init__
	Constructor.
def	get_compact_display
	Returns the compact_display field of a CommutativeOperation.
def	get_info
	Allow the subclasses to access this field.
def	get_first_letter
	If the Product is literal, returns the first factor's letter.
def	get_sign
	Returns the sign of the first element of the CommutativeOperation.
def	set_info
	Sets the info field of the CommutativeOperation.
def	set_sign
	Sets the sign of the first element of the CommutativeOperation.
def	set_compact_display
	Sets a value to the compact_display field.
def	evaluate
	Returns the value (number) of an numerically evaluable CommutativeOperation.
def	dbg_str
	Raw display of the CommutativeOperation (debugging method)
def	__len__
	Returns the number of elements of the CommutativeOperation.
def	contains_exactly
	True if the CommutativeOperation contains exactly the given objct It can be used to detect objects embedded in this CommutativeOperation.
def	contains_a_rounded_number
	To check if this contains a rounded number...
def	append
	Appends a given element to the current CommutativeOperation.
def	remove
	Removes a given element from the current CommutativeOperation.
def	throw_away_the_neutrals
	Returns self without the equivalent-to-a-single-neutral elements.
def	is_displ_as_a_single_neutral
	True if the object can be displayed as a single neutral element.
def	is_displ_as_a_single_numeric_Item
	True if the CommutativeOperation contains only one numeric Item.
def	is_displ_as_a_single_int
	True if the object can be displayed as a single int.
Public Attributes
	str_openmark
	str_closemark
Properties
	info = property(get_info, doc="info field of a CommutativeOperation")
	compact_display

Detailed Description

Abstract mother class of Product and Sum.

Gathers common methods.

Definition at line 3725 of file base_calculus.py.

Constructor & Destructor Documentation

def core.base_calculus.CommutativeOperation.__init__ ( self )

Constructor.

Warning:: CommutativeOperation objects are not really usable

Returns:: An "instance" of CommutativeOperation

Reimplemented from core.base_calculus.Operation.

Definition at line 3736 of file base_calculus.py.

References core.base_calculus.CommutativeOperation._compact_display, core.base_calculus.CommutativeOperation._info, core.base_calculus.CommutativeOperation.str_closemark, and core.base_calculus.CommutativeOperation.str_openmark.

Referenced by core.calculus.Equation.__init__(), and core.root_calculus.Value.substitute().

Member Function Documentation

def core.base_calculus.CommutativeOperation.append	(	self,
		elt
	)

Appends a given element to the current CommutativeOperation.

Parameters:

elt	The element to append (assumed to be a Exponented)

Definition at line 4004 of file base_calculus.py.

Referenced by core.base_calculus.Polynomial.__init__().

def core.base_calculus.CommutativeOperation.contains_a_rounded_number ( self )

To check if this contains a rounded number...

Returns:: True or False

Reimplemented from core.root_calculus.Evaluable.

Definition at line 3989 of file base_calculus.py.

def core.base_calculus.CommutativeOperation.contains_exactly	(	self,
		objct
	)

True if the CommutativeOperation contains exactly the given objct It can be used to detect objects embedded in this CommutativeOperation.

Parameters:

objct The object to search for

Returns:: True if the CommutativeOperation contains exactly the given objct

Reimplemented from core.root_calculus.Evaluable.

Definition at line 3974 of file base_calculus.py.

References core.base_calculus.Operation.element.

Referenced by core.base_calculus.CommutativeOperation.remove().

def core.base_calculus.CommutativeOperation.dbg_str	(	self,
		options
	)

Raw display of the CommutativeOperation (debugging method)

Parameters:

options : info='OK' let dbg_str display more info

Returns:: A string : "<info1|info2||factor0, ..., factorn>^{exponent}" or : "[info1|info2||term0, ..., termn]^{exponent}"

Reimplemented in core.base_calculus.Polynomial, and core.base_calculus.Monomial.

Definition at line 3928 of file base_calculus.py.

References core.base_calculus.CommutativeOperation.compact_display, core.base_calculus.Operation.element, core.base_calculus.CommutativeOperation.info, core.base_calculus.CommutativeOperation.str_closemark, core.base_calculus.CommutativeOperation.str_openmark, core.base_calculus.Operation.symbol, and core.base_calculus.Quotient.symbol.

def core.base_calculus.CommutativeOperation.evaluate	(	self,
		options
	)

Returns the value (number) of an numerically evaluable CommutativeOperation.

Returns:: The result as a number

Definition at line 3855 of file base_calculus.py.

Referenced by core.base_calculus.Product.calculate_next_step(), core.base_calculus.Sum.expand_and_reduce_next_step(), core.base_calculus.Sum.is_null(), core.base_calculus.Product.reduce_(), and core.base_calculus.Sum.reduce_().

def core.base_calculus.CommutativeOperation.remove	(	self,
		elt
	)

Removes a given element from the current CommutativeOperation.

Parameters:

elt	The element to remove (assumed to be a Exponented)

Definition at line 4016 of file base_calculus.py.

References core.base_calculus.CommutativeOperation.contains_exactly(), core.base_calculus.Item.dbg_str(), core.base_calculus.SquareRoot.dbg_str(), core.base_calculus.Quotient.dbg_str(), core.base_calculus.Fraction.dbg_str(), core.base_calculus.CommutativeOperation.dbg_str(), and core.base_calculus.Operation.element.

def core.base_calculus.CommutativeOperation.set_compact_display	(	self,
		arg
	)

Sets a value to the compact_display field.

Parameters:

arg	Must be True or False

Definition at line 3840 of file base_calculus.py.

References core.base_calculus.CommutativeOperation._compact_display.

Property Documentation

core::base_calculus.CommutativeOperation::compact_display [static]

Initial value:

property(get_compact_display,
                        doc="compact_display field of a CommutativeOperation")

Definition at line 3800 of file base_calculus.py.

Referenced by core.base_calculus.Product.calculate_next_step(), core.base_calculus.CommutativeOperation.dbg_str(), core.base_calculus.Product.get_factors_list(), core.base_calculus.Product.into_str(), core.base_calculus.Sum.into_str(), core.base_calculus.Product.is_reducible(), and core.base_calculus.Sum.requires_brackets().

The documentation for this class was generated from the following file:

mathmaker_dev/core/base_calculus.py

Public Member Functions

Public Attributes

Properties

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Property Documentation