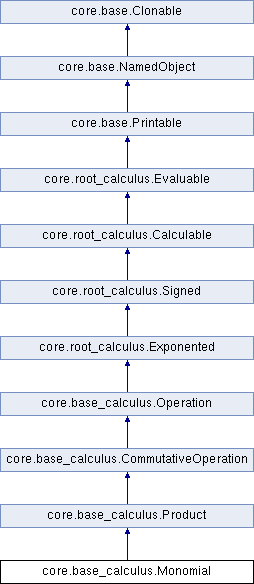
A Monomial is a Product of a numeric Exponented and a literal Item. More...

Inheritance diagram for core.base_calculus.Monomial:

Public Member Functions
def	__init__
	Constructor.
def	get_sign
	Gets the sign of the Monomial.
def	get_coeff
	Returns the numeric coefficient of the Monomial.
def	get_raw_value
	Gets the value of a Monomial of degree 0.
def	get_first_letter
	Returns the letter of the Monomial.
def	get_degree
	Returns the degree of the Monomial (i.e.
def	get_value_inside
	Gets the Value of the Monomial, just to mimic the case when it is of degree 0.
def	set_letter
	Sets the letter of the Monomial.
def	set_degree
	Set the degree of the Monomial.
def	set_coeff
	Set the degree of the Monomial.
def	dbg_str
	Raw display of the Monomial (debugging method)
def	is_null
	True if it's the null Monomial.
def	is_numeric
	True if Monomial's degree is 0 or ZERO_POLYNOMIAL_DEGREE.
def	is_positive
	True if Monomial's coefficient's sign is '+'.
def	is_negative
	True if Monomial's coefficient's sign is '-'.
Properties
	sign = property(get_sign, doc = "Monomial's sign")
	coeff = property(get_coeff, doc = "Monomial's coefficient")
	raw_value = property(get_raw_value, doc = "0-degree-Monomial's value")
	degree = property(get_degree, doc = "Monomial's degree")
	letter = property(get_first_letter, doc = "Monomial's letter")
	value_inside

Detailed Description

A Monomial is a Product of a numeric Exponented and a literal Item.

Definition at line 7521 of file base_calculus.py.

Constructor & Destructor Documentation

def core.base_calculus.Monomial.__init__	(	self,
		arg,
		options
	)

Constructor.

Warning:: Might raise an UncompatibleType exception.

Parameters:

arg

DEFAULT|Monomial|(sign, coeff, degree)|....... Possible arguments are :

DEFAULT, which is equivalent to ('+', 1, 0)
another Monomial which will be copied
(sign, coeff, degree) where coeff is a number and degree an integer
(coeff, degree) where coeff's numeric Exponented & degree an integer
(RANDOMLY, max_coeff, max_degree) where max_* are integers A Monomial will always be by default compact displayed (i.e. 2x and not 2×x). If the argument isn't of the kinds listed above, an exception will be raised.

options

any option Options can be :

randomly_plus_signs_ratio : will be effective only in the case of (RANDOMLY, max_coeff, max_degree) arg. In this case, the random choice of the sign of the Monomial will respect the given ratio

Returns:: A instance of Monomial

Definition at line 7549 of file base_calculus.py.

Referenced by core.calculus.Equation.__init__(), and core.root_calculus.Value.substitute().

Member Function Documentation

def core.base_calculus.Monomial.dbg_str	(	self,
		options
	)

Raw display of the Monomial (debugging method)

Parameters:

options No option available so far

Returns:: A string containing " << coeff × X ^ degree>> "

Reimplemented from core.base_calculus.CommutativeOperation.

Definition at line 7771 of file base_calculus.py.

References core.base_calculus.Monomial.degree, core.base_calculus.Item.exponent, core.root_calculus.Exponented.exponent, and core.base_calculus.Fraction.exponent.

def core.base_calculus.Monomial.get_coeff ( self )

Returns the numeric coefficient of the Monomial.

Returns:: The numeric coefficient of the Monomial

Definition at line 7664 of file base_calculus.py.

References core.base_calculus.Product.factor.

def core.base_calculus.Monomial.get_degree ( self )

Returns the degree of the Monomial (i.e.

exponent of factor[1])

Returns:: The degree of the Monomial

Definition at line 7698 of file base_calculus.py.

References core.base_calculus.Product.factor.

def core.base_calculus.Monomial.get_first_letter ( self )

Returns the letter of the Monomial.

Returns:: The letter of the Monomial

Reimplemented from core.base_calculus.CommutativeOperation.

Definition at line 7687 of file base_calculus.py.

References core.base_calculus.Product.factor.

Referenced by core.root_calculus.Evaluable.alphabetical_order_cmp(), and core.root_calculus.Value.into_str().

def core.base_calculus.Monomial.get_raw_value ( self )

Gets the value of a Monomial of degree 0.

Warning:: Raises an error if asked on non-degree-0 Monomial

Returns:: value_inside.raw_value

Definition at line 7676 of file base_calculus.py.

References core.base_calculus.Item.value_inside, and core.base_calculus.Monomial.value_inside.

def core.base_calculus.Monomial.get_sign ( self )

Gets the sign of the Monomial.

Returns:: The sign of the Monomial This can't be done by CommutativeOperation.get_sign() apparently. Maybe check exactly why, some day

Reimplemented from core.base_calculus.CommutativeOperation.

Definition at line 7650 of file base_calculus.py.

References core.base_calculus.Product.factor, core.base_calculus.Item.is_null(), core.base_calculus.SquareRoot.is_null(), core.base_calculus.Quotient.is_null(), core.base_calculus.Product.is_null(), core.base_calculus.Sum.is_null(), and core.base_calculus.Monomial.is_null().

Referenced by core.base_calculus.Fraction.calculate_next_step(), core.base_calculus.Sum.requires_inner_brackets(), core.base_calculus.Fraction.set_down_numerator_s_minus_sign(), core.root_calculus.Signed.set_opposite_sign(), and core.root_calculus.Value.set_opposite_sign().

def core.base_calculus.Monomial.get_value_inside ( self )

Gets the Value of the Monomial, just to mimic the case when it is of degree 0.

Returns:: value_inside

Definition at line 7710 of file base_calculus.py.

References core.base_calculus.Item._value_inside, core.base_calculus.Function._value_inside, and core.base_calculus.Monomial._value_inside.

def core.base_calculus.Monomial.is_negative ( self )

True if Monomial's coefficient's *sign* is '-'.

Todo:: How to answer to the question if this Monomial is null ?

Reimplemented from core.root_calculus.Signed.

Definition at line 7831 of file base_calculus.py.

References core.base_calculus.Operation.element.

Referenced by core.base_calculus.Item.get_minus_signs_nb(), core.base_calculus.SquareRoot.get_minus_signs_nb(), and core.base_calculus.Item.requires_inner_brackets().

def core.base_calculus.Monomial.is_positive ( self )

True if Monomial's coefficient's *sign* is '+'.

Todo:: How to answer to the question if this Monomial is null ?

Reimplemented from core.root_calculus.Signed.

Definition at line 7819 of file base_calculus.py.

References core.base_calculus.Operation.element.

Referenced by core.base_calculus.Item.evaluate().

Property Documentation

core::base_calculus.Monomial::value_inside [static]

Initial value:

property(get_value_inside,
                            doc = "0-degree Monomial's Value inside")

Definition at line 7727 of file base_calculus.py.

Referenced by core.base_calculus.Monomial.get_raw_value().

The documentation for this class was generated from the following file:

mathmaker_dev/core/base_calculus.py

Public Member Functions

Properties

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Property Documentation