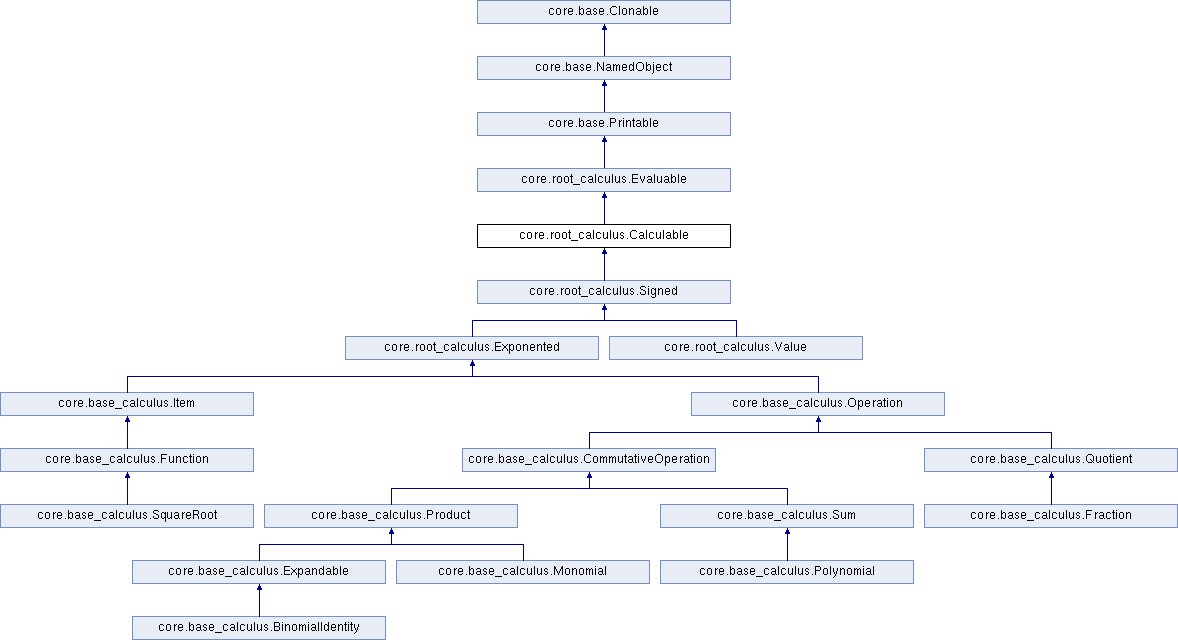
Abstract mother class of all (calculable) mathematical objects It is not possible to implement any Calculable object. More...
Public Member Functions | |
| def | get_iteration_list |
| Returns the list of elements to iter over. | |
| def | calculate_next_step |
| Returns the next Calculable object during a numeric calculation. | |
| def | expand_and_reduce_next_step |
| Returns the next step of expansion/reduction of the Sum So, either the Sum of its expanded/reduced terms, or the Sum itself reduced, or None. | |
| def | __len__ |
| Returns the number of elements of the Exponented. | |
| def | __iter__ |
| This will iter over the content of the Calculable. | |
| def | next |
| def | multiply_symbol_is_required |
| True if the usual writing rules require a × between two factors. | |
| def | requires_brackets |
| True if the argument requires brackets in a product For instance, a Sum with several terms or a negative Item. | |
| def | requires_inner_brackets |
| True if the argument requires inner brackets The reason for requiring them is having an exponent different from 1 and several terms or factors (in the case of Products & Sums) | |
| def | substitute |
| Uses the given lexicon to substitute literal Values in self. | |
| def | is_displ_as_a_single_1 |
| True if the object can be displayed as a single 1 For instance, the Product 1×1×1×1 or the Sum 0 + 0 + 1 + 0. | |
| def | is_displ_as_a_single_int |
| True if the object can be displayed as a single int. | |
| def | is_displ_as_a_single_minus_1 |
| True if the object can be displayed as a single -1 For instance, the Product 1×1×(-1)×1 or the Sum 0 + 0 - 1 + 0. | |
| def | is_displ_as_a_single_0 |
| True if the object can be displayed as a single 0 For instance, the Product 0×0×0×0 (but not 0×1) or the Sum 0 + 0 + 0 (but not 0 + 1 - 1) | |
| def | is_displ_as_a_single_numeric_Item |
| True if the object is or only contains one numeric Item. | |
| def | is_displ_as_a_single_neutral |
| True if the object can be considered as a neutral element. | |
Detailed Description
Abstract mother class of all (calculable) mathematical objects It is not possible to implement any Calculable object.
Definition at line 177 of file root_calculus.py.
Member Function Documentation
| def core.root_calculus.Calculable.expand_and_reduce_next_step | ( | self, | |
| options | |||
| ) |
Returns the next step of expansion/reduction of the Sum So, either the Sum of its expanded/reduced terms, or the Sum itself reduced, or None.
- Returns:
- Exponented
Reimplemented in core.base_calculus.BinomialIdentity, core.base_calculus.Expandable, core.base_calculus.Sum, core.base_calculus.Product, core.base_calculus.Fraction, core.base_calculus.SquareRoot, and core.base_calculus.Item.
Definition at line 207 of file root_calculus.py.
| def core.root_calculus.Calculable.multiply_symbol_is_required | ( | self, | |
| objct, | |||
| position | |||
| ) |
True if the usual writing rules require a × between two factors.
- Parameters:
-
objct The other one position The position (integer) of self in the Product
- Returns:
- True if the writing rules require × between self & obj
Reimplemented in core.base_calculus.Sum, core.base_calculus.Product, core.base_calculus.Quotient, core.base_calculus.SquareRoot, and core.base_calculus.Item.
Definition at line 244 of file root_calculus.py.
| def core.root_calculus.Calculable.requires_brackets | ( | self, | |
| position | |||
| ) |
True if the argument requires brackets in a product For instance, a Sum with several terms or a negative Item.
- Parameters:
-
position The position of the object in the Product
- Returns:
- True if the object requires brackets in a Product
Reimplemented in core.base_calculus.Sum, core.base_calculus.Product, core.base_calculus.Quotient, core.base_calculus.SquareRoot, and core.base_calculus.Item.
Definition at line 258 of file root_calculus.py.
True if the argument requires inner brackets The reason for requiring them is having an exponent different from 1 and several terms or factors (in the case of Products & Sums)
- Returns:
- True if the object requires inner brackets
Reimplemented in core.base_calculus.Sum, core.base_calculus.Product, core.base_calculus.Quotient, core.base_calculus.SquareRoot, and core.base_calculus.Item.
Definition at line 271 of file root_calculus.py.
The documentation for this class was generated from the following file:
- mathmaker_dev/core/root_calculus.py
 1.7.6.1
1.7.6.1